A PROPOS  DE LA VULGARISATION
                                                              « C’est une grande misère que de n’avoir pas assez                                                               d’esprit pour parler ni assez de jugement                                                                pour se taire. »                                                                                                                                                                                                                                                  (Jean de la Bruyère, caractères)
 
 
Préliminaires.
« Lire une traduction c’est regarder l’envers d’un tapis. » (Cervantès)
 
Il se  pourrait dire que l’allégorie de la caverne de  Platon est une généralisation de cette pensée de Cervantès.
Plus généralement, cela revient à confondre l’objet avec son ombre et bien souvent, voir une ombre suffit à beaucoup  pour croire connaître l’objet !
C’est le cas pour les lecteurs d’ouvrages de vulgarisation en physique. J’entends ici la physique au sens large : physique classique, Relativité restreinte et générale, mécanique quantique, astrophysique et cosmologie. Je rappelle que la physique classique contient la mécanique rationnelle, la mécanique céleste, la thermodynamique, la théorie de la cinétique des gaz, l’optique, l’électricité, le magnétisme  …
Le grand philosophe grec Platon situait la mathématique dans son « Monde des Idées », dans le « logos » comme l’appelait son continuateur Plotin.
Galilée disait déjà en son temps : « La Nature parle le langage mathématique »
Plus tard, Descartes abondait  dans son sens ainsi que Newton et Leibniz.
De nos jours, il ne se trouve plus de physiciens ni de mathématiciens pour nier que l’Univers EST mathématique, par exemple les physiciens et mathématiciens Alain Connes et Roger Penrose autoproclamés avec force platoniciens..
Le grand physicien américain Max Tegmark prétend lui que la Mathématique EST l’Univers.
De nos jours, la physique a atteint des sommets inconcevables autrefois. La Relativité restreinte, la Relativité générale, ont bouleversé notre conception newtonienne de l’espace et du temps. la mécanique quantique a chamboulé la théorie de la mesure, la cosmologie, grâce à la Relativité générale, nous a appris que l’Univers a une histoire et est peut-être fermé avec une courbure positive.
Mais toutes ces théories sont écrites dans le langage de l’Univers, à savoir le langage mathématique.
Ce langage est-il traduisible dans une langue  naturelle, telle que le français par exemple ?
 
Sur la vulgarisation.
La physique « classique » (newtonienne).
Cette physique est elle aussi mathématisée. Mais elle n’est pas, en général, contre-intuitive et sa vulgarisation, cantonnée dans un domaine pas trop compliqué est relativement possible pour donner une idée de ses découvertes.
Mais à condition de ne pas se risquer à vulgariser n’importe quoi ! Par exemple  considérons l’importante notion thermodynamique d’entropie.
Simplement la mesure de l’entropie  S d’un système isolé fait immédiatement appel à la formule : S = klog(V) où k est la constante de Boltzmann, et log(V) est le logarithme du volume du plus grand compartiment de l’espace des phases du système.
Bien souvent, le vulgarisateur se contente de définir l’entropie comme une mesure du désordre. Mais il manque le plus important : Montrer que l’entropie d’un système isolé est croissante et c’est précisément ce résultat qui est important.
Alors ? Vulgariser la physique classique ? Oui, mais modérément !
 
La Relativité.
La Relativité restreinte.
Cette théorie étant totalement contre-intuitive échappe déjà à toute tentative de vulgarisation bien que sa mathématique, du moins dans sa partie mécanique, est relativement simple. Il n’en est pas de même dans sa partie électrodynamique.
Le germe de cette théorie se trouve dans une des quatre équations de Maxwell unifiant le magnétisme et l’électricité.
En effet, un terme de cette équation montre que la vitesse de la lumière se déduit de la constante relative à la permittivité du vide et de la constante de la perméabilité magnétique du vide. La vitesse de la lumière ne dépendant que de deux constantes est nécessairement elle-même une constante, c’est-à-dire que cette vitesse est indépendante de tout repère animé d’un mouvement rectiligne uniforme (Repère galiléen appelé aussi repère inertiel).
C’est cette invariance de la vitesse de la lumière qui a entrainé la révolution de notre conception de l’espace et du temps, lesquels perdaient leur caractère absolus.
Mais bien que la mathématique de la Relativité restreinte soit relativement facile, elle n’en requiert pas moins de bonnes connaissances en mathématiques permettant de comprendre la théorie de l’espace-temps quadridimensionnel  de Minkowski ainsi que la vertu  heuristique de son « cône de lumière ».
Aussi, on ne peut donner que des résultats de cette théorie sans pouvoir expliquer comment on les a obtenus.  
Il existe pourtant une exception : On peut mathématiquement expliquer la dilatation du temps en fonction de la vitesse v d’un corps matériel.
Cette formule est : t’ = t√(1-v²/c²) où t’ est le temps dilaté d’un corps animé de la vitesse v par rapport au temps t d’un corps au repos. (voir fgure ci-dessous  
Pour comprendre la démonstration (voir dessin ci-dessous) il suffit de savoir qu’une distance est le produit d’un temps par une vitesse et de connaître le théorème de Pythagore ! C’est tout. Hélas, il n’en est pas de même pour les autres résultats de la Relativité restreinte.
 

 
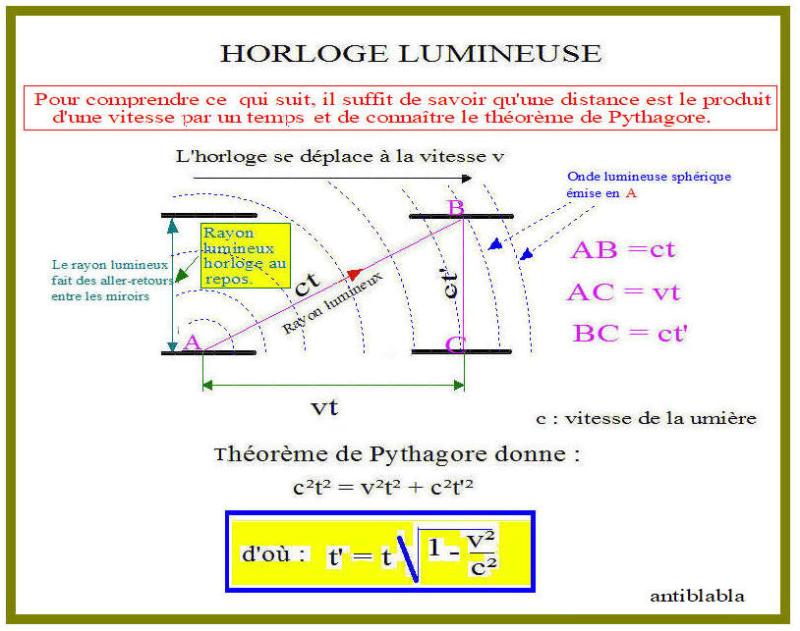
J’ai écrit ci-dessus que seuls les résultats peuvent être donnés.
Et encore ! Car ces résultats sont contre-intuitifs et il ne faut pas s’étonner qu’ils soient niés bêtement, notamment par les 9% de Français qui croient la Terre plate et les 29% qui soutiennent mordicus que le soleil tourne autour de la Terre.
 
 
 
 
La Relativité générale.
Alors que la Relativité restreinte traite des corps animés d’un mouvement rectiligne uniforme, la théorie de la Relativité générale prend en compte l’accélération de ces corps. C’est avant tout une théorie de la gravitation.
Dans cette théorie, la gravitation est le résultat du fait qu’un corps massif courbe l’espace-temps dans son voisinage et ce, d’autant plus que ce corps est massif.
Dans cette théorie, l’outil mathématique fondamental est l’analyse tensorielle et l’espace de Riemann, théories totalement hors de portée de toute personne dépourvue d’un fort bagage mathématique.
C’est à partir de son équation tensorielle fondamentale que furent prédites et vérifiées les découvertes :
 
     -    La théorie du Big bang,
- De l’expansion de l’Univers.
- L’explication de l’avance du périhélie de Mercure,
- De la déviation d’un rayon lumineux passant près d’un corps massif.
- De l’effet « Lens-Thirring »  
- De l’existence des trous noirs, (Déjà entrevue par Simon de Laplace)
- De la découverte des ondes de gravitation.
- Et j’en oublie …
 
Et quand on pense qu’Einstein est simplement parti de ce principe appelé « principe d’équivalence »:
« Tout champ de gravitation est localement équivalent à un champ d’accélération », on reste pantois d’admiration pour ce génie ! »
 
Quoi qu’il en soit, on ne peut vulgariser la Relativité générale et même ses résultats s’expriment dans un langage mal compris et qui déforme en plus la réalité.
 
 
 
La mécanique quantique.
« Toute personne qui étudie la mécanique quantique et n’est pas saisie de vertige n’y a rien compris »(Niels Bohr)
Voilà qui commence bien !
« Personne ne comprend la mécanique quantique » (Richard Feynman)
Y a-t-il contradiction entre ces deux remarques ? Que nenni !
Simplement, ici, le mot « comprendre » est pris dans deux sens différents.
Chez Niels Bohr, un des pères fondateurs avec Louis de Broglie, Heisenberg, Schrödinger, Born, etc, il s’agissait seulement de comprendre la mathématique de cette discipline, alors que chez Feynman, il s’agissait de l’interprétation de cette mathématique, ce qui est fondamentalement différent.
Plusieurs tentatives d’interpréter les équations de la mécanique quantiques sont encore de nos jours en compétition :
L’interprétation :
 
- de Copenhague,
- Théorie des états relatifs, aussi appelée « théorie de mondes multiples ».
- Théorie des histoires cohérentes, (Griffits)
- Théorie de la décohérence (Roland Omnès et al.)
- et quelques autres moins connues.
 
Richard Feynman déclarait à ses élèves : « Les fentes d’Young et le spin des particules constituent ce qu’il y a de plus quantique dans le monde quantique ».
Passons sur les fentes d’Young qui sont beaucoup plus complexes qu’on le pourrait croire et où la vulgarisation exerce ses ravages.
La situation est la même pour ce qui concerne le spin des particules dont l’orientation « haut » ou « bas » ou « à gauche » ou « à droite » etc.. désigne en fait des orientations de « vecteurs d’état » dans l’espace de Hilbert.
Dans cet espace, un spin « haut » et un spin « bas »sont orthogonaux !
Là encore toute tentative de vulgariser ce concept de spin est vouée à l’échec et ne peut donner que des idées fausses au lecteur non averti.
Mais le comble de l’inconscience est atteint lorsqu’un ignorant de la théorie prétend expliquer l’intrication quantique. Là ça frise la fumisterie !
Que faut-il répondre à la question : « Qu’est-ce que l’intrication quantique ». ?
Prenons deux électrons par exemple, l’un de fonction d’onde Ψ1 et l’autre de fonction d’onde Ψ2 (lettre grecque PSI)
Eh bien, il faut répondre ceci :
L’intrication quantique de ces deux électrons est : |Ψ> = α| Ψ 1>  +  β|Ψ2> où α et β sont des nombres complexes.
On comprend (avec un fort bagage en mathématique), ce que dit cette expression, mais on ne sait pas ce qu’elle SIGNIFIE ! Pour s’en tirer, on dit que la mécanique quantique est une théorie non locale et le tour est joué.
On remarquera en passant qu’apparaissent dans cette expression la fonction d’onde Ψ. Mais d’où vient Ψ ? Eh bien c’est une solution de l’équation différentielle de Schrödinger dépendante du temps qu’il faut connaître ainsi que savoir la résoudre ! (Il en existe une autre indépendante du temps)
De plus, la notation (de Paul Dirac) |Ψ>, qui s’énonce « ket de psi »  est un vecteur d’état dans l’espace de Hilbert supposée connue la théorie de ces espaces !
Hélas, ces exemples parmi tant d’autres  montrent bien l’impossibilité de vulgariser, au sens habituel du terme, la mécanique quantique. Je dis au sens habituel, car de grands physiciens ont avec succès, « vulgarisé » cette science mais n’ont pu éviter de se placer sur un niveau exigeant quelques développements mathématiques. Voir les ouvrages de Roger Penrose, de Roland Omnès etc. par exemple.
 
L’astrophysique,
Cette discipline, du moins en partie, est plus accessible au profane d’un niveau en physique élémentaire.
On peut lui faire comprendre comment on obtient la distance des étoiles proches par leur parallaxe, la distance des étoiles plus lointaines grâce aux céphéides et aussi par la mesure de l’effet Doppler, aux étoiles encore plus lointaines à l’aide des supernovae de type Ia.
Mais là où ça se complique, c’est l’obtention de la distance des galaxies très lointaines par leur z. car l’effet Doppler n’est plus dû à la vitesse propre de la galaxie mais à la vitesse d’expansion de l’Univers.  
Dans l’effet Doppler classique, on a z = v/c mais pour les galaxies très lointaines, on a z = Re/Rr – 1 où Re représente le rayon de l’Univers lors de l’émission du rayon lumineux et Rr ce rayon à la réception de ce rayon lumineux. Bien sûr, cette formule ne permet pas de calculer z mais explique pourquoi on peut avoir z > 1 à cause de la vitesse d’expansion de l’Univers à de telles distances.
On peut aussi expliquer comment on apprend la température de surface des étoiles par la loi de déplacement de Wien, leur champ magnétique par l’effet Zeeman etc.
Mais la vulgarisation tombe en panne dès que l’on traite des étoiles à neutrons et, a fortiori, des trous noirs, l’étude de ces derniers étant du domaine de la Relativité générale.
 
 
La cosmologie.
On peut dire que la cosmologie est la fille ainée de la théorie de la Relativité générale ce qui ne facilite certes pas sa vulgarisation !
Paradoxalement, le modèle cosmologique standard tentant de décrire l’Univers à sa naissance se révèle être le tombeau de la Relativité générale !
En effet, en deçà du temps de Planck, il est indispensable  de faire intervenir des phénomènes quantiques, ce qui signifie qu’il  est inévitable de trouver une théorie unifiant Relativité générale et mécanique quantique.
Pour l’instant, c’est l’échec. Oh, ce n’est pas les théories proposées en cosmologie qui manquent pour l’unification ou non :
 
- Théorie des cordes, des supercordes, M-Theory,
- Théorie de la gravitation quantique à boucles,
- Théorie ER = EPR,
- Théorie de la géométrie non commutative,
- Théorie technicolor,
- Théorie holographique,
- Théorie de la quintessence,
- Etc.
 
Mais toutes ces théories ont un point commun : Elles exigent l’emploi des hautes mathématiques ! Et à mon grand regret !
En effet, la théorie des supercordes exige un fort bagage en topologie différentielle, théorie dont j’ignore tout et je me garderais bien d’expliquer ce qu’il en est ! Cette théorie fait intervenir une notion topologique déjà rencontrée en topologie générale (que je connais) mais traitée en topologie différentielle que je ne peux comprendre. Il s’agit de la « transition de flop » qui montre que l’espace peut se déchirer.
De nombreux points de ce que l’on appelle « le modèle standard cosmologique » sont en cours de révision :e
 
-      L'inflation,-  
-      Accélération de l’expansion : uniforme ou locale ?
- Matière noire,
- Energie noire,
- Univers fermé ou ouvert ?
- Univers précédé d’un autre Univers ?
- Multivers ?
- Théorie MOND (MOdified Newton Dynamics)
 
Bref, toutes ces recherches se font à un niveau de mathématiques accessible à bien peu de spécialistes.
Je dirais bien que j’y perds mon latin pour certaines, mais je me console en me disant que je ne peux perdre ce que je n’ai pas appris !
Et puis, comme l’a dit le grand Aristote :  
« Le plus grand des savoirs est de savoir qu’on ne sait pas. »
 
In memoriam.
                                       
Je veux conclure cette partie en rendant hommage au regretté professeur Jean Claude Pecker, de l’Académie des sciences, professeur au Collège de France,  grand astrophysicien français qui a porté hautes dans le monde les couleurs de l’astrophysique française. Il nous a quitté en décembre 2019.
Je lui dois tout.
C’est lui qui m’a initié à la méthode scientifique laquelle exige une grande probité intellectuelle qui consiste, entre autres, à pouvoir dire tranquillement « Je me suis trompé » ou encore « Je ne sais pas » tous ces aveux qui ont beaucoup de mal à sortir du gosier des ignorants !  
C’est encore lui qui m’a appris à faire de la recherche, qui m’a prévenu de son caractère ingrat : Pour une bonne vingtaine d’idées il est fréquent qu’une seule soit la bonne et même parfois toutes sont à jeter !
Adieu donc Jean  Claude Pecker, je ne vous oublierai jamais.

Jean-Claude Pecker nous a quitté le 20 février 2020, merci de faire preuve d'un peu plus de rigueur

https://www.academie-sciences.fr/fr [...] ecker.html

 
 
Oui, c'est vrai. C'est fin décembre que son état s'est brusquement aggravé et j'ai été bouleversé. Ayant appris son décès je l'ai bêtement daté de décembre.
Mais hélas, cette erreur ne le fait pas revenir parmi nous, et se révèle être une bien pauvre maladresse eut égard de la perte d'un astrophysicien qui s'est illustré dans le monde entier pour ses travaux sur le soleil.
 
Oui, j'ai très bien connu Jean Claude Pecker, ayant réalisé, par vacation du CNRS, une recherche sous sa  direction, et surtout sous ses conseils, sur un calcul conduisant à mieux connaître les abondances
 de molécules diatomiques dans la photosphère du Soleil.
Ce fut à la Faculté des Sciences de Clermont-Ferrand pendant l'année scolaire 1954-1955.
 
Enfin, j'apprécie votre rectification mais moins de me reprocher mon manque de rigueur alors que ce ne fut qu'une inexcusable distraction. Scientifique moi-même, je ne pense pas manquer de rigueur dans l'exercice de mes travaux, du moins lorsque j'étais en activité, étant retraité de nos jours. Âgé de presque 93 ans, puissiez-vous n'être pas  plus distrait lorsque vous aurez mon âge, âge que je vous souhaite sincèrement d'atteindre avec des neurones en aussi bon état que les miens. .