Bonjour à tous.
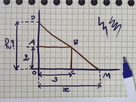
Un charpentier a tracé à main levé le profil d'un étage sous les toits laissant libre un espace rectangulaire OABC. Il souhaite étudier la hauteur h en fonction de la largeur du sol x. Sur son schéma, les longueurs sont exprimées en mètres.
On appelle f la fonction qui à x associe la hauteur h.
J'ai mis l'image du schéma avec le post.
La premère question : Expliquer pourquoi x est strictement supérieur à 3.
Voici ce que j'ai fait :
On a une fonction f qui est définie sur R+ diffèrent de 0.
Donc h(x) = 2 + AD.
Ensuite je ne sais quoi faire ...
Pourriez-vous m'éclairer ? Svp
---------------
C. Coshy
